| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- dp
- bronze4
- gradle설정
- 뷰클래스
- toLong()
- Kotlin
- 프로그래머스
- 백준
- LIS
- 테마변경
- 녹음기
- stack
- naver open api
- bronze3
- LV1
- silver4
- RETROFIT
- Android
- bottom-up
- Alert Dialog
- Silver5
- map
- 임시저장하기
- silver3
- fragment에서 context사용
- Top-Down
- bronze2
- recyclerView 클릭이벤트
- 다크모드제한
- RecyclerView
- Today
- Total
유니 코드
[BOJ/백준][Silver1] 11052: 카드 구매하기(Kotlin) 본문
문제
요즘 민규네 동네에서는 스타트링크에서 만든 PS카드를 모으는 것이 유행이다.
PS카드는 PS(Problem Solving)분야에서 유명한 사람들의 아이디와 얼굴이 적혀있는 카드이다. 각각의 카드에는 등급을 나타내는 색이 칠해져 있고, 다음과 같이 8가지가 있다.
- 전설카드
- 레드카드
- 오렌지카드
- 퍼플카드
- 블루카드
- 청록카드
- 그린카드
- 그레이카드
카드는 카드팩의 형태로만 구매할 수 있고, 카드팩의 종류는 카드 1개가 포함된 카드팩, 카드 2개가 포함된 카드팩, ... 카드 N개가 포함된 카드팩과 같이 총 N가지가 존재한다.
민규는 카드의 개수가 적은 팩이더라도 가격이 비싸면 높은 등급의 카드가 많이 들어있을 것이라는 미신을 믿고 있다. 따라서, 민규는 돈을 최대한 많이 지불해서 카드 N개 구매하려고 한다. 카드가 i개 포함된 카드팩의 가격은 Pi원이다.
예를 들어, 카드팩이 총 4가지 종류가 있고, P1 = 1, P2 = 5, P3 = 6, P4 = 7인 경우에 민규가 카드 4개를 갖기 위해 지불해야 하는 금액의 최댓값은 10원이다. 2개 들어있는 카드팩을 2번 사면 된다.
P1 = 5, P2 = 2, P3 = 8, P4 = 10인 경우에는 카드가 1개 들어있는 카드팩을 4번 사면 20원이고, 이 경우가 민규가 지불해야 하는 금액의 최댓값이다.
마지막으로, P1 = 3, P2 = 5, P3 = 15, P4 = 16인 경우에는 3개 들어있는 카드팩과 1개 들어있는 카드팩을 구매해 18원을 지불하는 것이 최댓값이다.
카드 팩의 가격이 주어졌을 때, N개의 카드를 구매하기 위해 민규가 지불해야 하는 금액의 최댓값을 구하는 프로그램을 작성하시오. N개보다 많은 개수의 카드를 산 다음, 나머지 카드를 버려서 N개를 만드는 것은 불가능하다. 즉, 구매한 카드팩에 포함되어 있는 카드 개수의 합은 N과 같아야 한다.
입출력
입력 : 첫째 줄에 민규가 구매하려고 하는 카드의 개수 N이 주어진다 (1 ≤ N ≤ 1,000) 둘째 줄에는 Pi가 P1부터 PN까지 순서대로 주어진다. (1 ≤ Pi ≤ 10,000)
출력 : 첫째 줄에 민규가 카드 N개를 갖기 위해 지불해야 하는 금액의 최댓값을 출력한다.
| 입력 | 출력 |
| 4 1 5 6 7 |
10 |
| 5 10 9 8 7 6 |
50 |
| 10 1 1 2 3 5 8 13 21 34 55 |
55 |
| 10 5 10 11 12 13 30 35 40 45 47 |
50 |
| 4 5 2 8 10 |
20 |
| 4 3 5 15 16 |
18 |
접근방법
이 문제는 일단 문제가 길었고 이해하기도 조금 어려웠었다,, (그도 그럴게 풀고나서 보니까 난이도가 silve1,,,,,ㅎㅎ)
지금까지 내가 풀던 dp문제와는 다른 느낌이었다
지금까지는 문제를 보고 노트에 적다보면 어떻게 풀어야될지 감이라도 왔는데 이 문제는 감 잡는데 한참 걸렸다
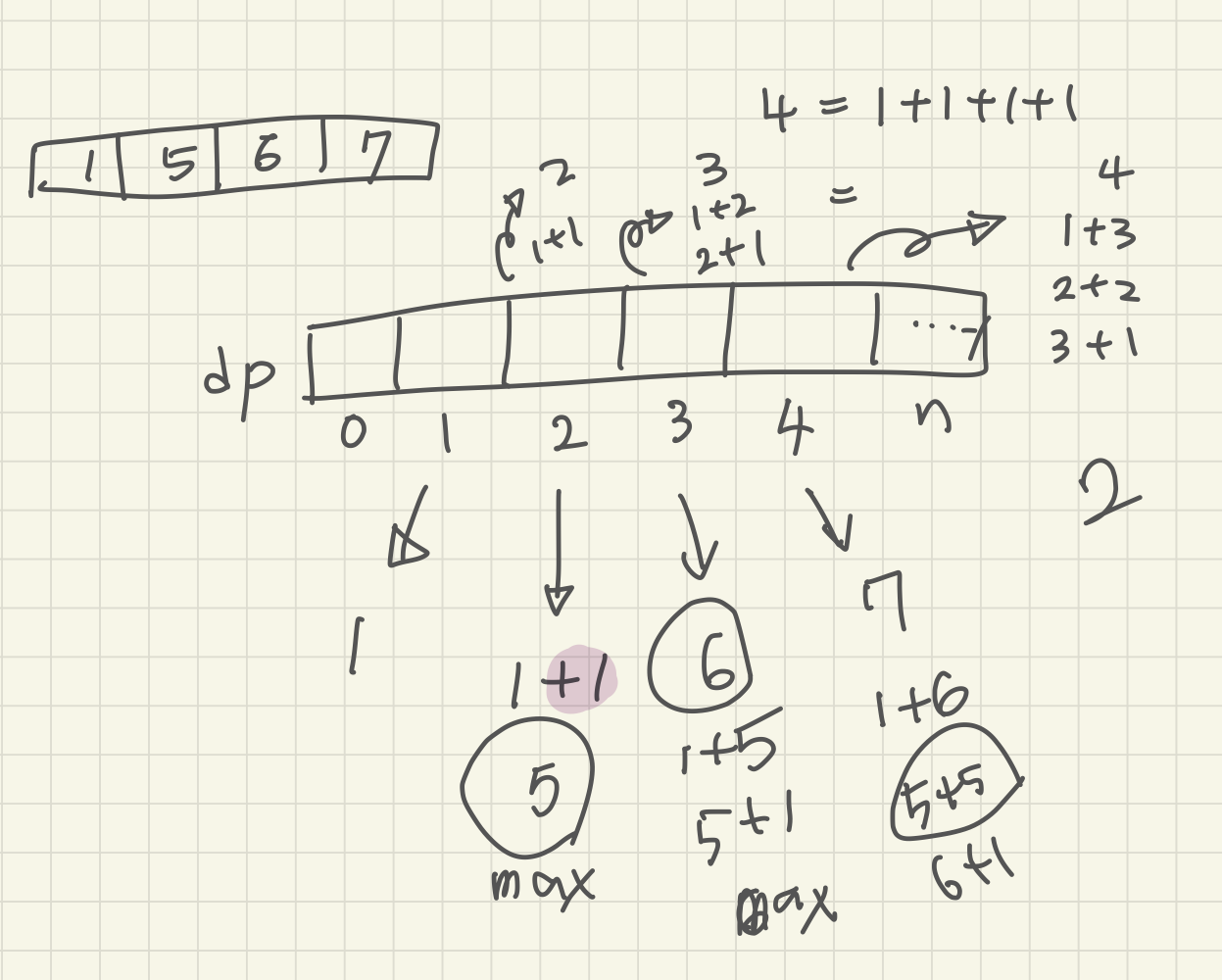
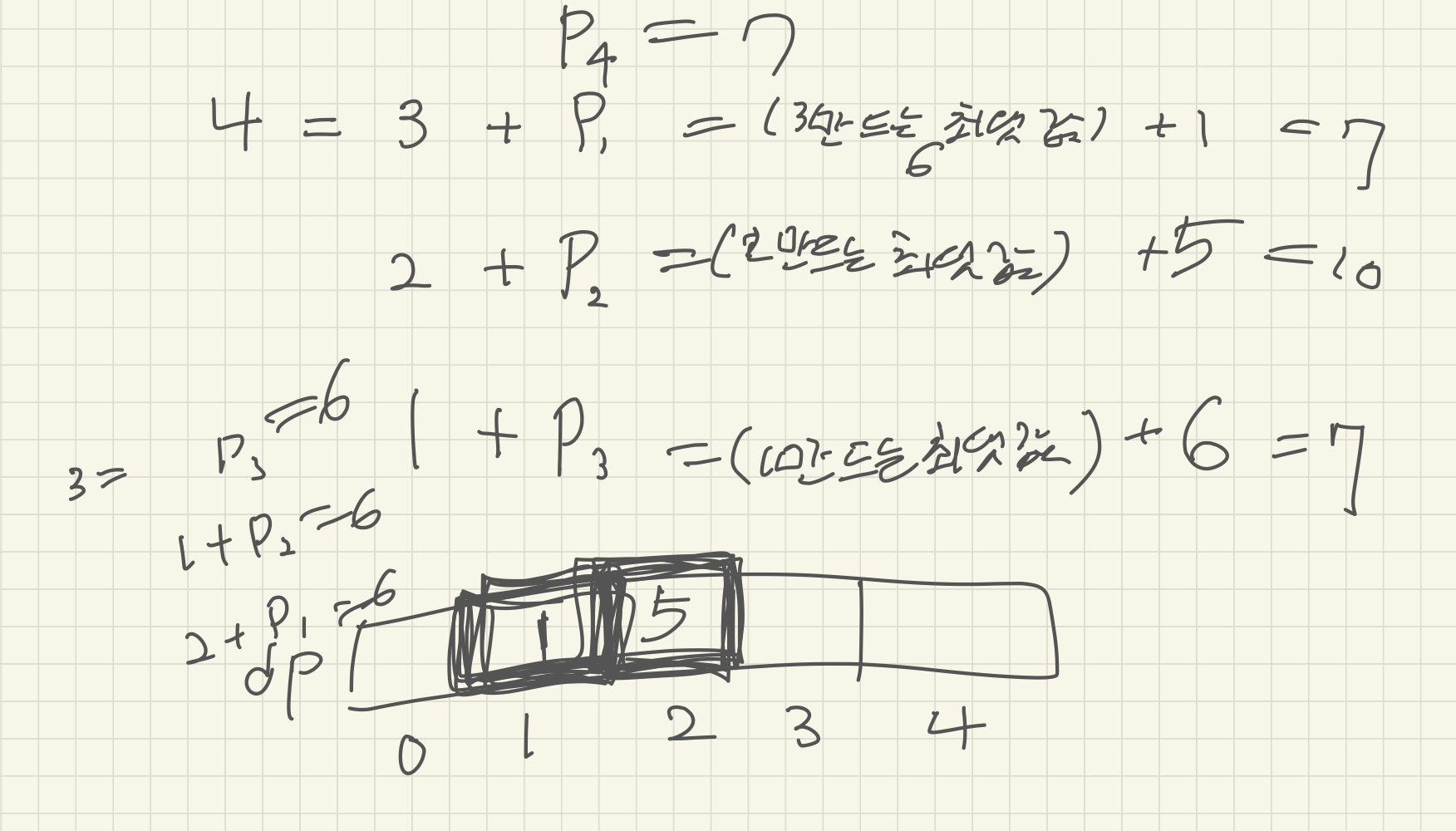
입력값 N이 4라고 가정하고 설명을 해보겠다(입출력 예제 1번)

dp배열은 각 index개의 카드를 사는 데 드는 비용의 최댓값이고
pay는 카드를 사는 데 드는 비용이 담긴 배열이다(그림에는 0부터 넣어줬는데 보기쉽게 Pi는 i인덱스에 저장하자)
먼저 카드 1장을 사는데 드는 최대비용은 P1이다
카드 2장을 사는데 드는 최대비용은 P2와 dp[1] + P1의 값을 비교하여 더 큰 값이 된다
카드 3장을 사는데 드는 최대비용은 P3와 dp[2] + P1, dp[1] + P2 중 가장 큰값이 된다
카드 4장을 사는데 드는 최대비용은 P4, dp[3] + P1, dp[2] + P2, dp[1] + P3 중 최댓값이 된다
이 문제는 각 dp값을 구할 때 식을 세우면 바로 값을 구할 수 있는 게 아니라
각각의 값들을 비교하여 최댓값을 구해야되서 어려웠다
어떻게 해야되나 생각을 계속 해보다가 이중반복문을 이용해서 최댓값을 구해야겠다고 생각했다
dp[n]의 값은 dp[n]과 dp[n - i] + pay[i]의 max를 구한다
아래 코드를 보자
코드
import java.util.*
import kotlin.math.max
fun main(){
val n = readLine()!!.toInt()
val pay = readLine()!!.split(" ").map{it.toInt()}
val list = IntArray(n + 1)
for(i in 0 until pay.size){
list[i + 1] = pay[i]
}
val dp = IntArray(n + 1){
if(it == 1) list[1]
else 0
}
for(i in 1..n){
for(j in 1..i){
dp[i] = max(dp[i], dp[i - j] + list[j])
}
}
println(dp[n])
}n : 구매할 카드의 수
pay : 각 카드팩 가격이 담긴 배열
list : pay배열은 0부터 값이 저장되니까 헷갈려서 인덱스를 뒤로 1개씩 밀어준 배열(편의상)
dp : n개의 카드를 구매하는데 드는 최대비용을 저장하는 배열
dp[1]은 카드팩1을 사는 비용이므로 dp[1] = list[1]로 초기화했고 나머지는 0으로 초기화함
1부터 n까지 dp값을 구해야 하니까 for문 사용
반복문 안에서 dp의 최댓값을 찾아야하니까 1부터 n까지 돌면서 dp[i]값과 dp[i - j] + list[j] 중 최댓값을 dp에 저장한다
이 문제는 정말 어려웠다..
이중 반복문을 사용했고, 배열을 사용해서 더 헷갈렸던 문제다
항상 인덱스가 잘 들어가는지 확인해야한다.. (확인 안하고 대충 되겠지 하고 채점 돌려서 틀렸,,,후)
그래도 silver1문제를 풀었다니 좀 뿌듯하다
좀 더 연습해서 gold문제도 풀고싶다!!
'알고리즘 > 다이나믹프로그래밍' 카테고리의 다른 글
| [BOJ/백준][Silver2] 11722. 가장 긴 감소하는 부분 수열(Kotlin) (0) | 2023.02.01 |
|---|---|
| [BOJ/백준][Silver2] 11053. 가장 긴 증가하는 부분 수열(Kotlin) (0) | 2023.02.01 |
| [BOJ/백준][Silver3] 11727: 2xn 타일링2(Kotlin) (0) | 2022.07.04 |
| [BOJ/백준][Silver3] 1003: 피보나치 함수(Kotlin) (0) | 2022.07.04 |




